Ya anteriormente les escribí un tutorial para instalar Ubuntu dentro de Windows, ahora este es un tutorial para hacer algo parecido desde Ubuntu. Se llama Wine, y no instala Windows en sí, mas bien es un programa que permite correr aplicaciones de Windows.

Definición según Wikipedia: es una re implementación de la interfaz de programación de aplicaciones de Win16 y Win32 para sistemas operativos basados en Unix. Permite la ejecución de programas diseñados para MS-DOS, y las versiones de Microsoft Windows 3.11, 95, 98, Me, NT, 2000, XP, Vista y 7.
Para una información completa en inglés, pueden visitar esta liga:
http://wiki.winehq.org/
Aquí el paso a paso para instalar y sacar lo mejor de Wine dese Ubuntu 11.04 (Natty Narwhal):
Abrir Terminal, y añadir los repositorios de wine:
sudo add-apt-repository ppa:ubuntu-wine/ppa
Instalar la actualización o nueva versión de wine con:
sudo apt-get update
sudo aptitude install wine
Para saber que version de wine tienes instalada puedes ejecutar:
wine --version (doble guion)
Al estar recien instalado no tenemos el directorio .wine así que ejecutamos:
winecfg
Se abre el asistente de configuración de wine, donde podemos seleccionar si queremos ejecutar wine a pantalla completa o como una ventana mas del escritorio, o el tipo de sonido que utilizamos. Al pulsar “Aceptar” se aplican los cambios de configuración y se crea nuestro directorio “.wine”.
Instalaremos un script llamado winetricks que nos instala muchas cosas que necesita el Windows.
Para usarlo, nos descargamos el script (para tenerlo a mano lo instalaremos en .wine):
cd
cd .wine
wget wget http://www.kegel.com/wine/winetricks
le damos permisos de ejecución:
chmod +x ./winetricks
Se instala de manera automática.
Se recomienda instalar las siguientes librerías:
DirectX 9 (imprescindibles para jugar a juegos):
./winetricks d3dx9
Las fuentes de texto droid que mejoran mucho la legibilidad en pantalla:
./winetricks droid
PhysX, el motor de fisicas PhysX (si dispones de alguna tarjeta Nvidia):
./winetricks physx
Metapaquete que instala un fuentes de texto (como Arial, Sans Serif, etc utilizadas en Windows):
./winetricks allfonts
Metapaquete que instala un montón de codecs para reproducir video y audio.
./winetricks allcodecs
- Fijo la version de sistema que emulo como Windows XP (esto también se hace desde winecfg):
./winetricks winxp
./winetricks sound=alsa
Renombrar la carpeta drive_c como harddiskvolume0 (que a veces es necesario en muchos instaladores):
./winetricks volnum
Deshabilitar GLSL usado por Direct3D:
./winetricks glsl-disable
Instalar librerías de Visual C 2008 (necesarias por algunos juegos):
./winetricks vcrun2008
Las librerias dcom (si dispones de la licencia de Windows 98):
./winetricks dcom98
Se puede instalar el framework NET 2.0 (requiere licencia):
./winetricks dotnet20
Puede que falte alguna DLL si eso pasa se muestra un error en la consola diciendo que te falta una DLL (nombre) y tendrás que bajarla y copiarla en tu
.wine/drive_c/windows/System32
Para facilitar la instalación, puede que necesites quitar o añadir alguna:
./winetricks d3dx9 droid winxp sound=alsa volnum vcrun2008 dotnet20 ie6 corefonts
Se ha añadido ie6 (internet explorer 6) y corefonts (fuentes de Windows).
Para la configuración de tarjeta 3D, hay 2 métodos:
Método 1: Para añadir claves al registro (lo harías exactamente igual que en Windows) ejecutando:
wine regedit
se abre el editor de registro y ya se puede cambiar las claves o añadir nuevas.
Una vez nos ha abierto el programa regedit , buscamos en la siguiente dirección:
HKEY_CURRENT_USER\Software\Wine\Direct3D
Las claves a añadir el caso de tener una tarjeta Nvidia para la key DIRECT3D son:
“DirectDrawRenderer”=”opengl”
“Nonpower2Mode”=”repack”
“OffscreenRenderingMode”=”fbo”
“RenderTargetLockMode”=”auto”
“UseGLSL”=”readtex”
“VertexShaderMode”=”hardware”
“VideoDescription”=”NVIDIA GeForce 8500 GT”
“VideoDriver”=”nv4_disp.dll”
“VideoMemorySize”=”256″
Las entradas que aparecen en negritas son las que cambiarían, dependiendo del modelo de la tarjeta. Las demás quedarían igual en todas las tarjetas Nvidia.
Método 2: Tambien se puede hacer de manera más rápida, ir al directorio .wine y editar un fichero llamado “
user.reg”, en ese fichero se van almacenando las claves del registro que va creando el usuario. Se edita el fichero, al final del mismo se pega el contenido:
sudo gedit /home/
"usuario ubuntu"/.wine/user.reg
en usuario ubuntu hay que poner el nombre de nuestro usuario en el sistema
[Software\\Wine\\Direct3D] 1258821033
"DirectDrawRenderer"="opengl"
"Nonpower2Mode"="repack"
"OffscreenRenderingMode"="fbo"
"RenderTargetLockMode"="auto"
"UseGLSL"="readtex"
"VertexShaderMode"="hardware"
"VideoDescription"="NVIDIA GeForce 8500 GT"
"VideoDriver"="nv4_disp.dll"
"VideoMemorySize"="256"
Para cualquier otra duda ó cambiar más parámetros,lo mejor es consultar la página web de wine: Wine HQ
Referencias:
http://wiki.winehq.org/FAQ
http://wiki.winehq.org/Debunking_Wine_Myths
http://morfeox69.blogspot.com/2011/05/instalar-wine-correctamente-en-ubuntu.html
http://wiki.winehq.org/ListofCommands


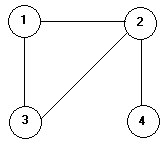

 Este es un árbol binario no equilibrado, o sea que no es AVL
Este es un árbol binario no equilibrado, o sea que no es AVL 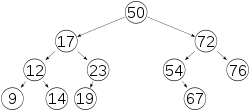 Este es un árbol binario equilibrado, o sea que si es AVL.
Este es un árbol binario equilibrado, o sea que si es AVL.




































